Trust Region Policy Optimization (TRPO)算法是由伯克利大学的Schulman等人于2015年提出的策略梯度(Policy Gradients)算法。TRPO通过最大化新策略相对于当前策略的优势来保证每次更新都是单调递增的(稳定),同时找到尽可能大的更新步幅。算法推导出的最终结果是在KL约束下最大化替代优势函数。
背景
考虑经典的 MDP\(<S, A, P, r, \rho_0, \gamma>\),其中 \(S\) 是所有状态(state)的集合,\(A\) 是所有动作(action)的集合,\(P: S\times A\times S \rightarrow \mathbb{R}\) 是转移概率分布,\(r\) 是奖励(reward)函数,\(\rho_0\) 是初始状态(\(s_0\))分布,\(\gamma\) 是折扣因子( discount factor)。
定义 \(\pi\) 为一个随机策略:\(\pi: S\times A\rightarrow [0, 1]\),定义 \(\eta(\pi)\) 来衡量策略 \(\pi\) 的好坏: \[ \eta(\pi)=\mathbb{E}_{s_0, a_0, ...\sim\pi}[\sum_{t=0}^\infty\gamma^tr(s_t)] \] 接着定义 state-action value function \(Q_\pi\), value function \(V_\pi\), 优势函数(advantage function)\(A_\pi\): \[ Q_\pi(s_t, a_t) = \mathbb{E}_{s_{t+1}, a_{t+1}, ...\sim\pi}[\sum_{l=0}^\infty\gamma^lr_{s_{t+l}}] \]
\[ V_\pi(s_t) =\mathbb{E}_{a_t, s_{t+1}, ...\sim\pi}[\sum_{l=0}^\infty\gamma^lr_{s_{t+l}}] \]
\[ A_\pi(s, a) = Q_\pi(s, a) - V_\pi(s) \]
然后可以通过下式来衡量策略 \(\tilde{\pi}\) 相对于策略 \(\pi\) 的优势(证明详见论文): \[ \begin{align} \eta(\tilde{\pi})&=\eta(\pi)+\mathbb{E}_{s_0, a_0, ...\sim\color{red}{\tilde{\pi}}}[\sum_{t=0}^\infty\gamma^tA_\pi(s_t,a_t)]\\ &= \eta(\pi)+\sum_s\color{red}{\rho_\tilde{\pi}(s)}\sum_a\tilde{\pi}(a|s)A_\pi(s, a) \end{align} \] 其中 \(\rho_\pi\) 为策略 \(\pi\) 的折扣访问频率(discounted visitation frequency): \[ \rho_\pi(s) = P(s_0=s)+\gamma P(s_1=s) + \gamma^2 P(s_2=s)+... \] 通过上式可知,只要每个状态 \(s\) 的期望优势非负,即 \(\sum_a\tilde{\pi}(a|s)A_\pi(s, a)>0\),就可以保证更新是单调非递减的,这其实就是经典的策略迭代(policy iteration)的更新方式。然而,由于 \(\rho_\tilde{\pi}(s)\) 的存在,导致直接优化上式很困难,所以引入一个替代优势(surrogate advantage): \[ \begin{align} L_\pi(\tilde{\pi})&=\eta(\pi)+\sum_s\color{red}{\rho_\pi(s)}\sum_a\tilde{\pi}(a|s)A_\pi(s, a)\\ \end{align} \] 经过一系列推导,可以得到策略 \(\tilde{\pi}\) 的优势下界: \[ \eta(\tilde{\pi})≥L_\pi(\tilde{\pi})-C\cdot D_{KL}^\max(\pi, \tilde{\pi}) \] 其中,\(C=\frac{4\epsilon\gamma}{(1-\gamma)^2}\),\(D_{KL}^\max\) 是最大的KL散度。
这里相当于对优化目标 \(L_\pi(\tilde{\pi})\) 进行了惩罚,惩罚因子为 \(C\),惩罚项为KL散度,目的是限制新旧策略的差距。通过最大化上述公式,就能最大化新策略 \(\tilde{\pi}\) 所得到的奖励,同时又不会离旧策略 \(\pi\) 太远(导致对当前数据过拟合),算法如下:

TRPO
由于Deep RL都是使用参数为 \(\theta\) 的神经网络来拟合策略 \(\pi_\theta\),为了使公式更简洁,把算法1中公式的 \(\pi\) 替换成 \(\theta\): \[ \theta = \arg\max_{\theta}[L(\theta_{old}, \theta)-C\cdot D_{KL}^\max(\theta_{old}|| \theta)] \] 其中, \[ \begin{align} L(\theta_{old}, \theta) &= \sum_s\rho_{\theta_{old}}(s)\sum_a\pi_\theta(a|s)A_{\theta_{old}}(s,a) \\ &= \mathbb{E}_{s,a\sim\pi_{\theta_{old}}}[\frac{\pi_\theta(a|s)}{\pi_{\theta_{old}}(a|s)}A_{\theta_{old}}(s,a)] \end{align} \] TRPO是算法1的近似,区别在于:TRPO没有使用惩罚项 \(C\),而是使用 KL散度约束(i.e. trust region constraint): \[ \theta = \arg\max_\theta L(\theta_{old}, \theta)\\ \text{ s.t. }\bar{D}_{KL}(\theta||\theta_{old})≤\delta \] 其中,\(\bar{D}_{KL}\) 是平均KL散度: \[ \bar{D}_{KL}(\theta||\theta_{old})=\mathbb{E}_{s\sim\pi_{\theta_{old}}}[D_{KL}(\pi_{\theta}(\cdot|s)||\pi_{\theta_{old}}(\cdot|s))] \] 然而上面的带约束优化也并非容易,所以TRPO对上式进行了一些近似,对目标函数和约束进行泰勒展开可以得到: \[ L(\theta_{old}, \theta) \approx g^T(\theta-\theta_{old}) \]
\[ \bar{D}_{KL}(\theta||\theta_{old})\approx \frac{1}{2}(\theta-\theta_{old})^TH(\theta-\theta_{old}) \]
其中,\(g\) 是替代函数的梯度在 \(\theta=\theta_{old}\) 处的值,凑巧的是,它和策略梯度的值正好相等:\(g = \triangledown_\theta J(\pi_\theta)|_{\theta_{old}}\);\(H\) 是对于 \(\theta\) 的海森矩阵(Hessian matrix)。
于是得到如下的近似优化问题: \[ \theta_{k+1}=\arg\max_\theta g^T(\theta-\theta_k)\\ \text{s.t. }\frac{1}{2}(\theta-\theta_k)^TH(\theta-\theta_k)≤\delta \] 通过拉格朗日法求解上述约束优化问题得: \[ \theta_{k+1}=\theta_k+\sqrt{\frac{2\delta}{g^TH^{-1}g}}H^{-1}g \] 这个就是 Natural Policy Gradient 的更新公式。不过,由于泰勒近似引入了误差,上式的解可能不满足 KL 约束,所以 TRPO 增加了一个线性搜索(backtracking line search): \[ \theta_{k+1}=\theta_k+\alpha^j\sqrt{\frac{2\delta}{g^TH^{-1}g}}H^{-1}g \] 其中,\(\alpha\in(0,1)\) 是回溯系数(backtracking coefficient),\(j\) 是最小的非负整数使得 \(\pi_{\theta_{k+1}}\) 满足 KL 约束并且产生正的替代优势,这样就可以保证训练进步是单调的。
最后,计算和存储 \(H^{-1}\) 的开销是很大的,尤其是神经网络的参数动不动就几M。TRPO 使用共轭梯度法(conjugate gradient)来解 \(Hx = g\),这样就不用直接计算和存储 \(H\)。
最终的更新公式为: \[ \theta_{k+1}=\theta_k+\alpha^j\sqrt{\frac{2\delta}{\hat{x}^TH\hat{x}}}\hat{x} \] 其中, \[ \begin{align} \hat{x}&\approx H^{-1}g & \text{(using conjugate gradient)} \end{align} \]
\[ H\hat{x} = \triangledown_\theta((\triangledown_\theta\bar{D}_{KL}(\theta||\theta_k))^T\hat{x}) \]
TRPO算法
Performance
TRPO的一些特点
- 保证每次更新在当前训练数据上都是进步的,训练过程更加稳定
- 通过满足KL约束来找尽可能大的步长
- on-policy 算法
- 可用于离散和连续的动作空间
- 算法较为复杂
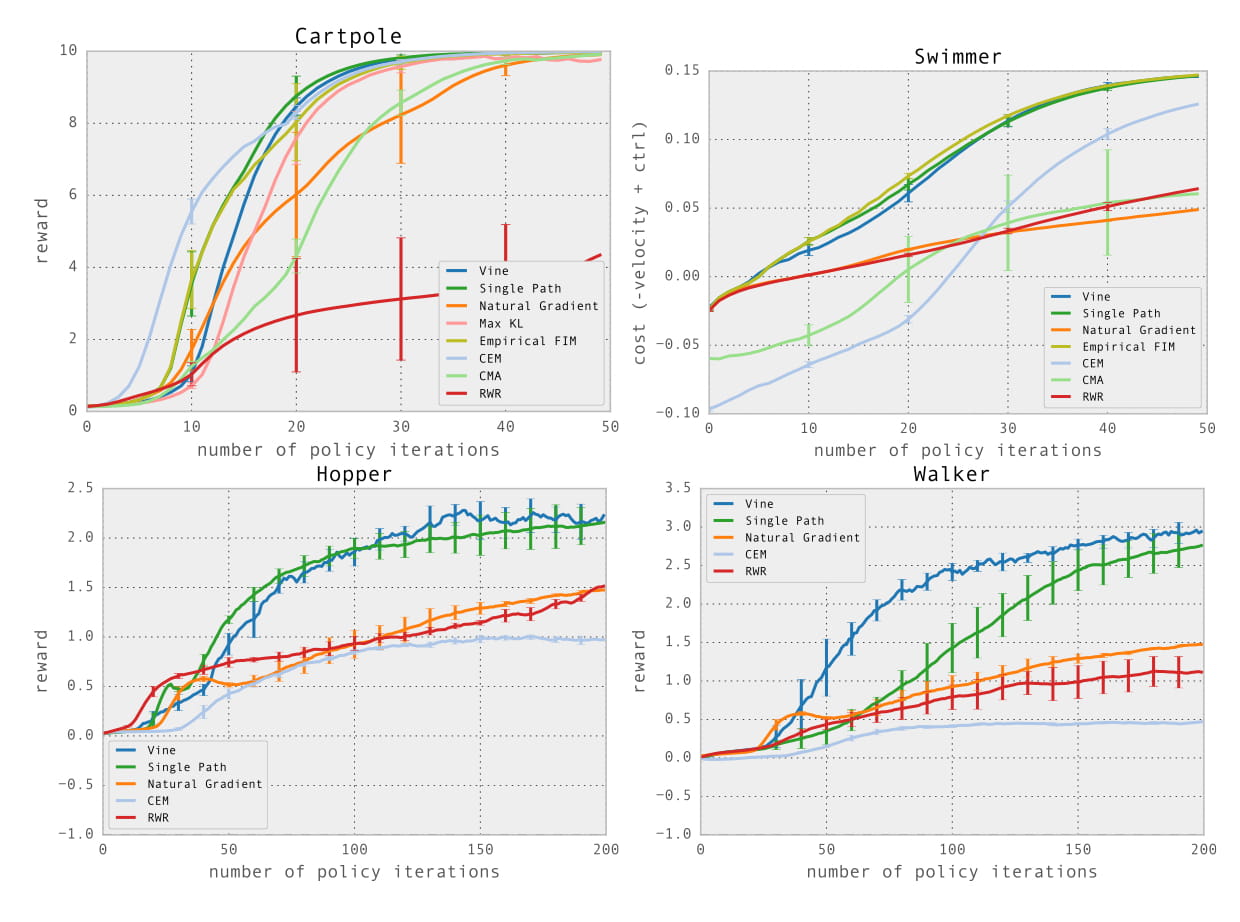
实验性能
在模拟机器人走路、游泳等任务中取得了在当时不错的效果;在通过视频输入玩Atari游戏的任务中表现不如DQN等方法。
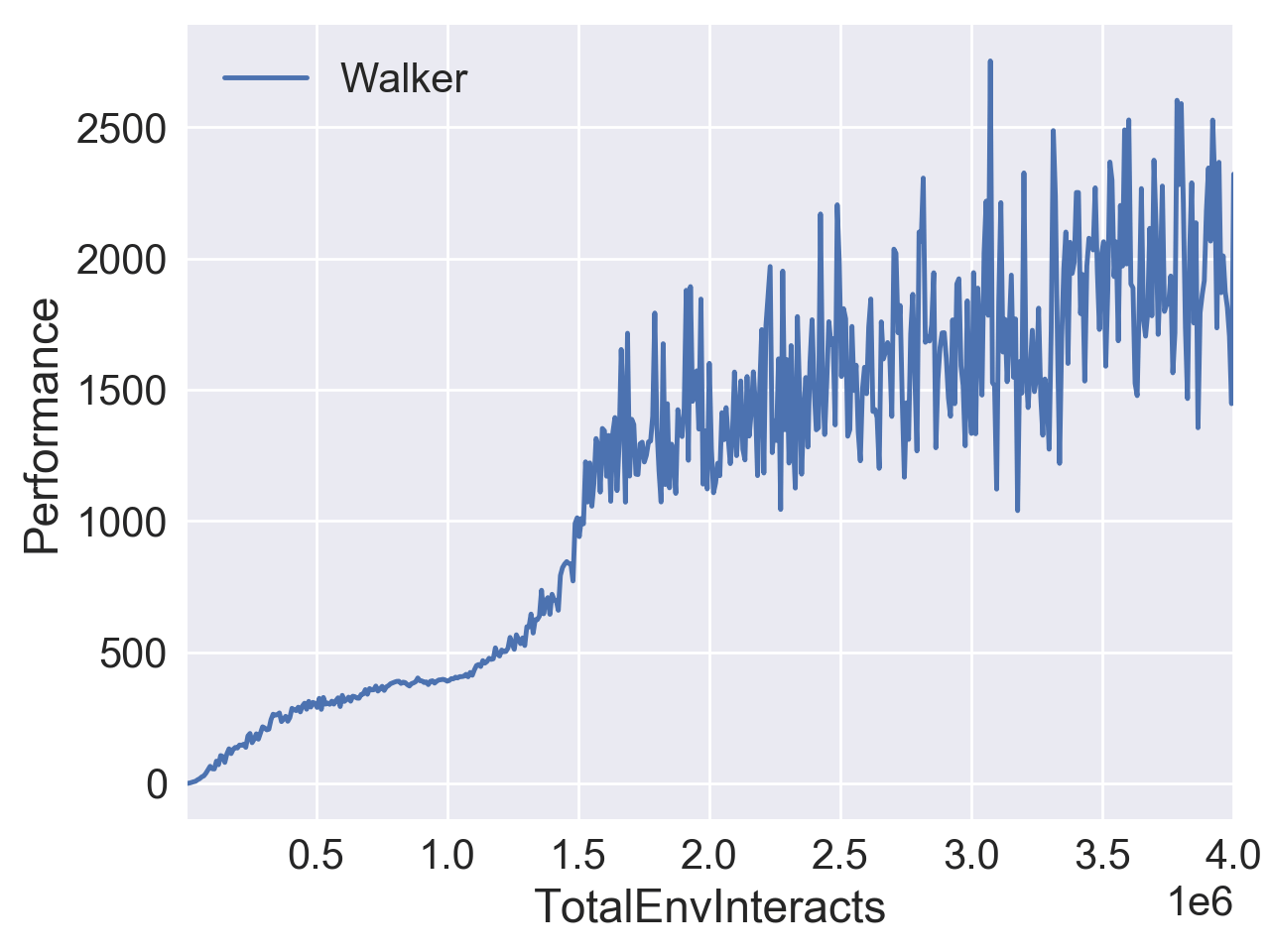
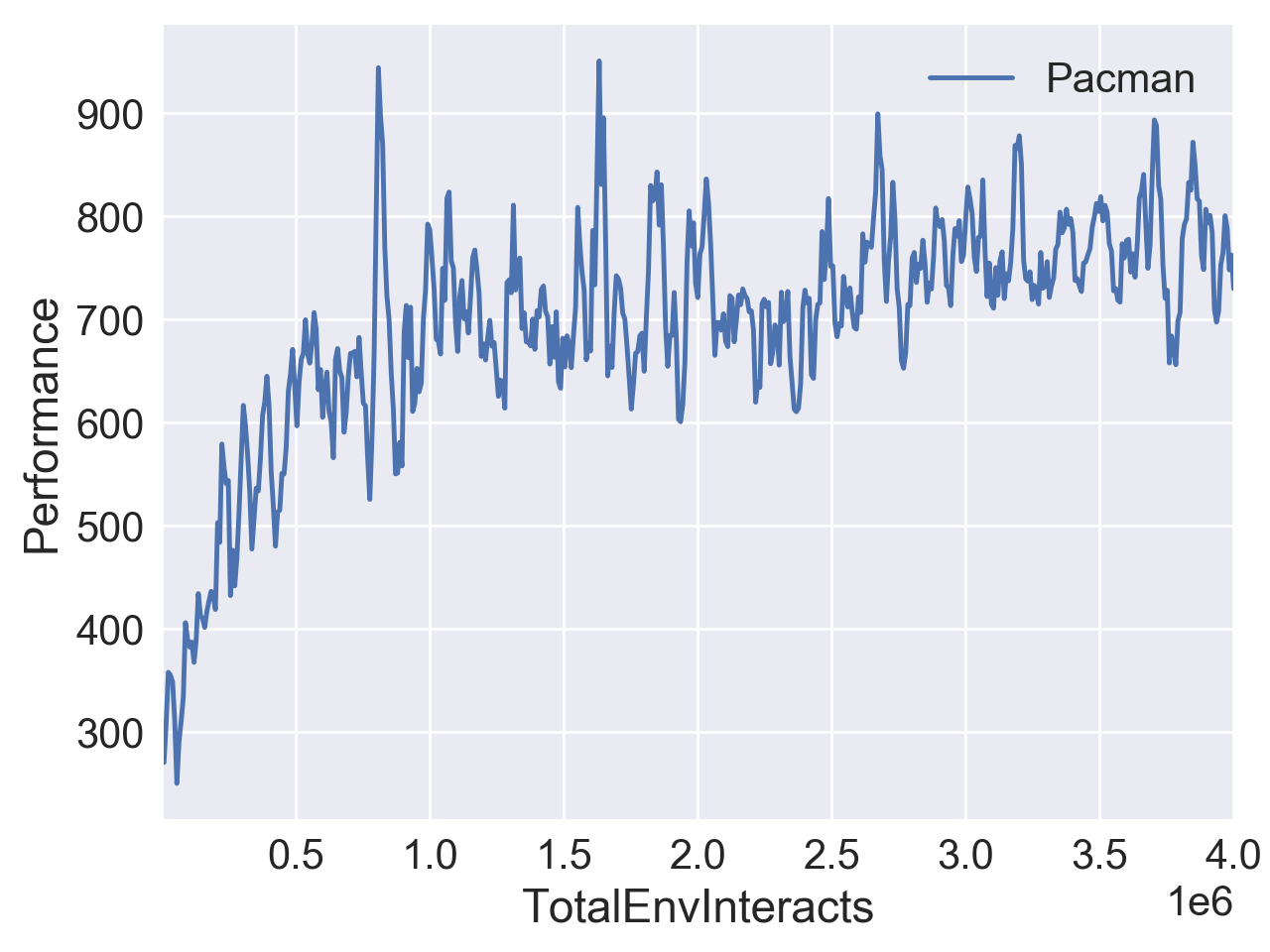
下图是我在 OpenAI Gym 的 Walker2d-v2 和 MsPacman-ram-v0 中测试的结果。
References
[1] https://arxiv.org/abs/1502.05477
[2] https://spinningup.openai.com/en/latest/algorithms/trpo.html
